Research interests

Random maps, graph theory, discrete geometry, enumerative and analytic combinatorics, statistical mechanics, integrable systems, topological recursion, quantum field theory, conformal field theory, computer algebra, branching processes,...


My favorite mathematical objects

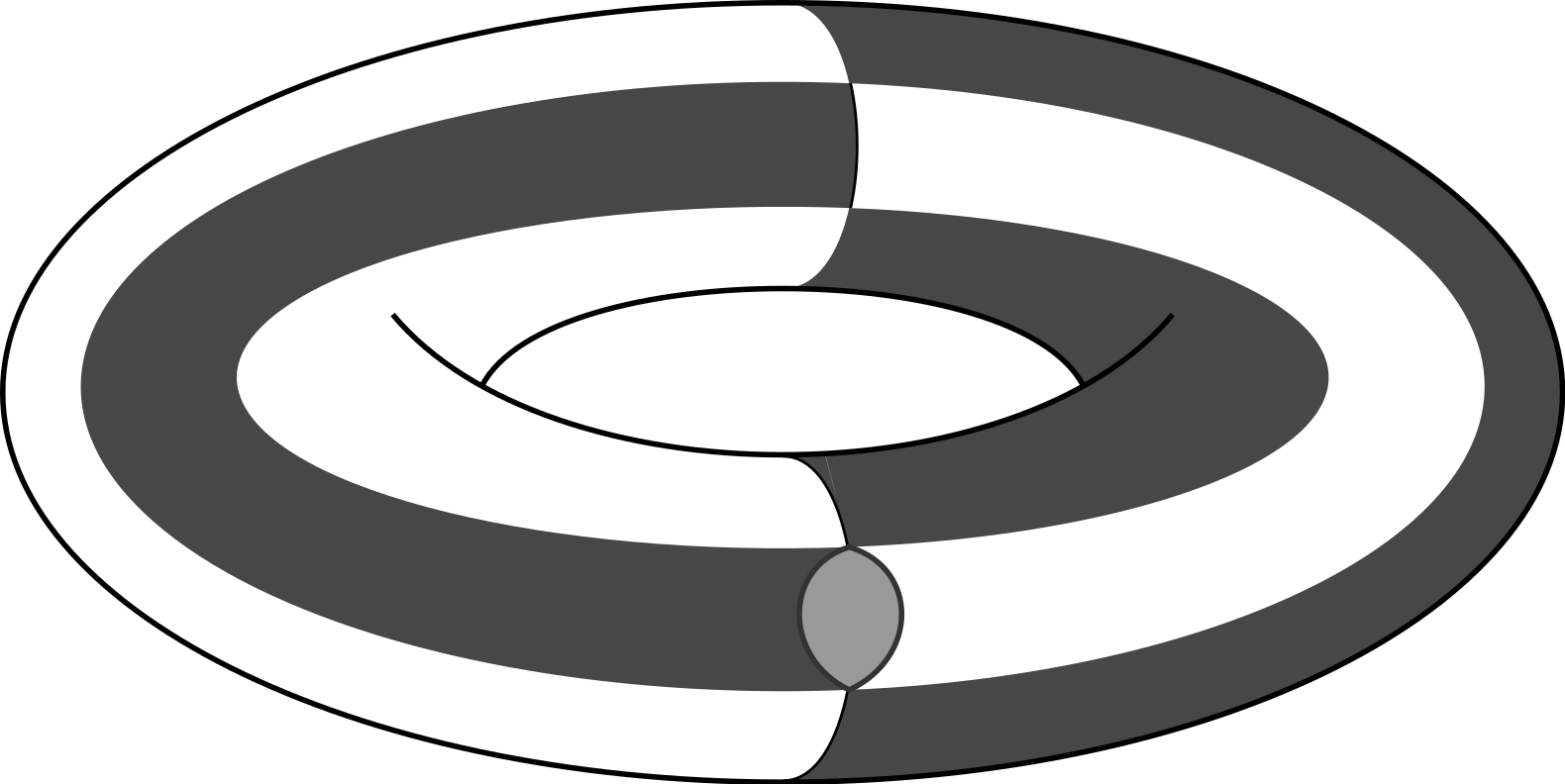
Random Colored Triangulations

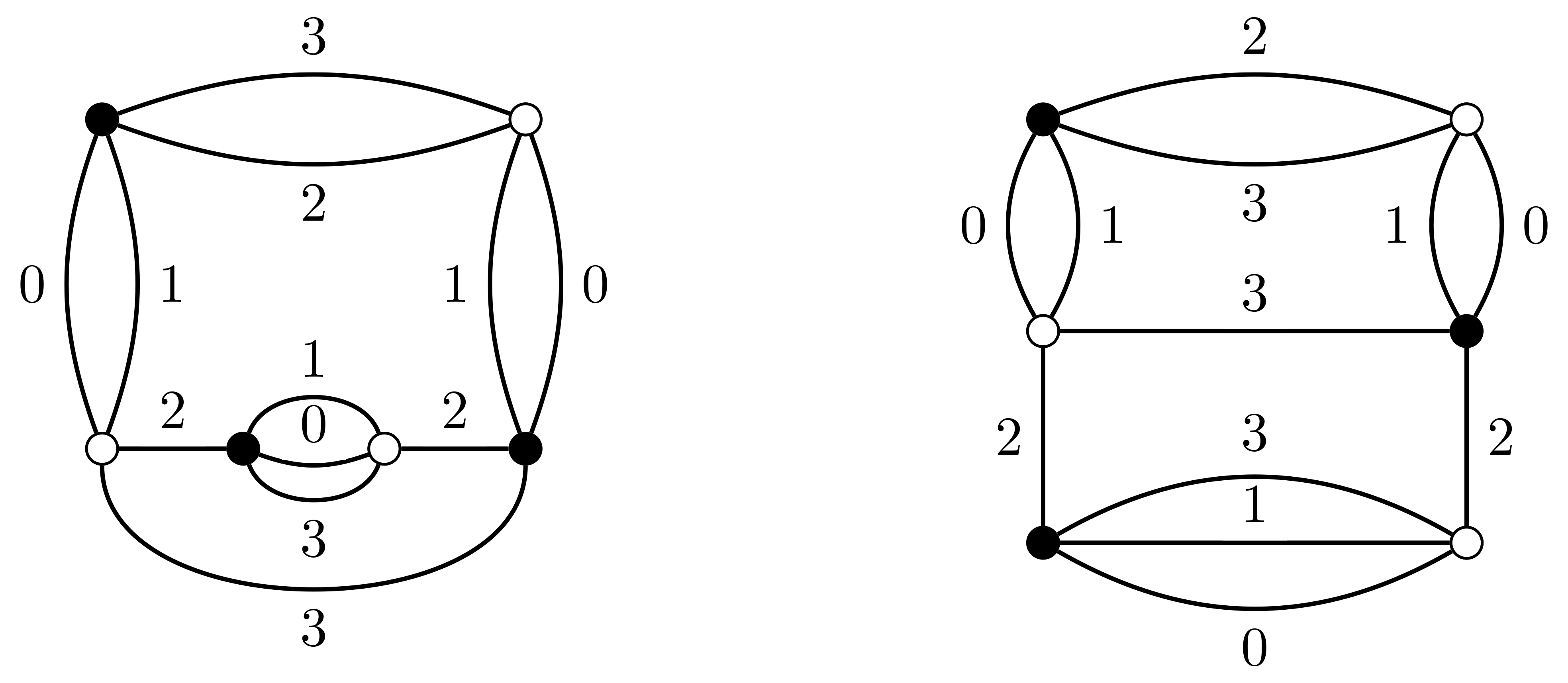
Colored graph

(D+1)-colored graphs are (D+1)-regular graphs, equipped with a proper (D+1)-coloring of their edges. (D+1)-colored graphs have been known from the 1970’s, and the work of Pezzana, to be an encoding of piecewise-linear (PL) topological structures, called colored trisps. These objects have garnered interest from theoretical physicists, starting with Gurau in 2010. Indeed, they are at the heart of a new approach to quantum gravity, colored tensor models, which generalizes some matrix models to higher dimensions. Through the study of probability distributions on (D+1)-colored graphs, we can thus define random colored trisps, and also get a better understanding of the quantized space-time described by colored tensor models.



Bicolored maps

Eulerian triangulation Eulerian quadrangulation

In dimension 2, 3-colored graphs of genus 0 are dual to bicolored triangulations, that is, planar maps whose faces are triangles that can be bicolored (in black and white for instance). Bicolored triangulations, by their coloration, have a richer structure than other families of maps such as usual triangulations. Another part of my research is devoted to the study of the combinatorial properties of bicolored triangulations, and of other classes bicolored maps, that are related in particular to the Ising model and to translation surfaces.