Domaines de recherche

Cartes aléatoires, théorie des graphes, géométrie discrète, combinatoire énumérative et analytique, mécanique statistique, systèmes intégrables, récurrence topologique, théorie quantique des champs, théorie conforme des champs, calcul formel, processus de branchement, ...


Mes objets mathématiques préférés

Triangulations colorées aléatoires

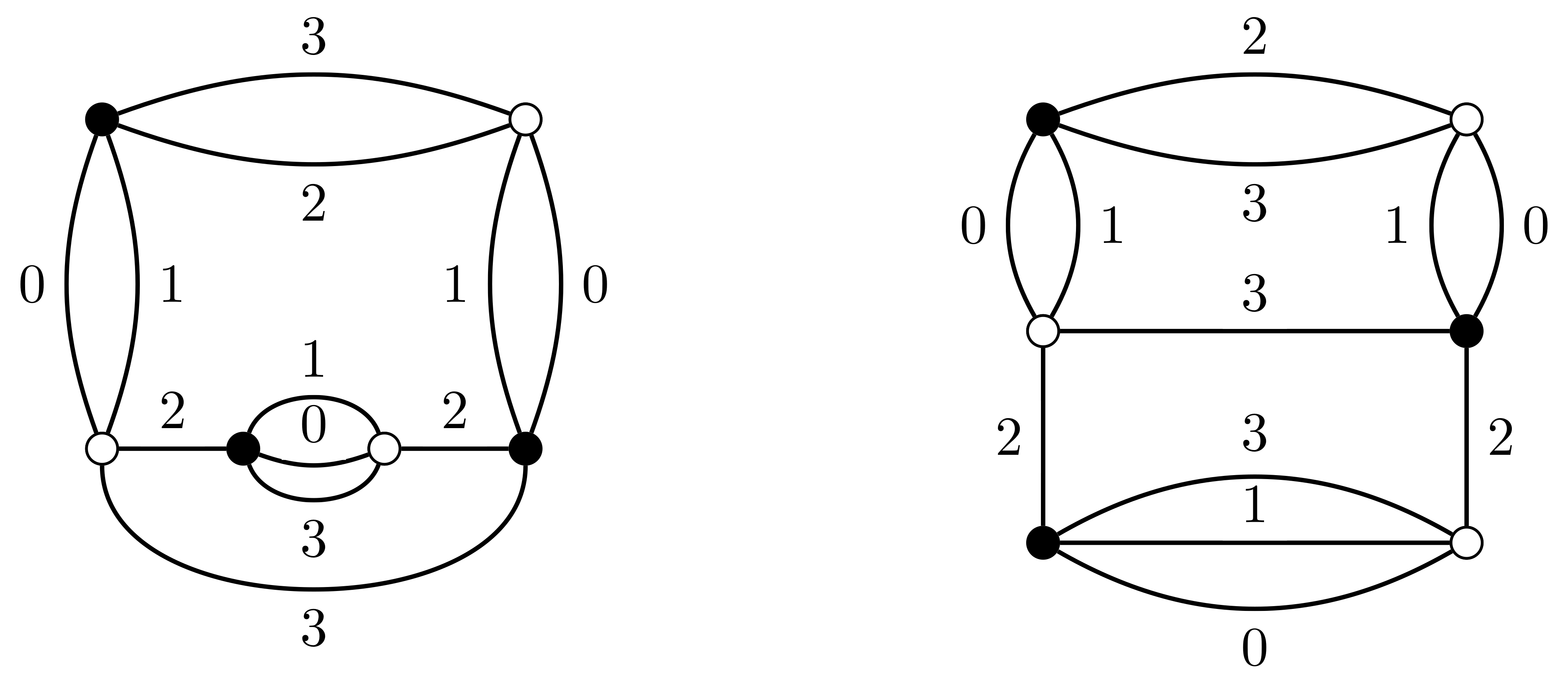
Colored graph

Les graphes (D+1)-colorés sont des graphes (D+1)-réguliers, munis d'une coloration propre de leurs arêtes avec D+1 couleurs. Pezzana a montré dans les années 1970 que les graphes (D+1)-colorés encodent des structures topologiques linéaires par morceaux (PL), appelés trisps colorés. Ces objets ont suscité l'intérêt de physiciens théoriciens, à commencer par Gurau en 2010. En effet, ils sont au cœur d'une nouvelle approche de la gravité quantique, les modèles de tenseurs colorés, qui généralise des modèles de matrices en dimensions supérieures. L'étude de distributions de probabilité sur les graphes (D+1)-colorés permet donc de définir des trisps colorés aléatoires, et aussi de mieux comprendre l'espace-temps quantifié décrit par les modèles de tenseurs colorés.



Cartes bicolorées

Eulerian triangulation Eulerian quadrangulation

En dimension 2, les graphes 3-colorés de genre 0 sont duaux des triangulations bicolorées, c'est-à-dire des cartes planaires dont toutes les faces sont des triangles, qu'on peut proprement bicolorer (en noir et blanc par exemple). Les triangulations bicolorées, de par leur coloration, ont une structure plus riche que d'autres familles de cartes comme les triangulations quelconques. Une autre partie de ma recherche est consacrée à l'étude des propriétés combinatoires des triangulations bicolorées, et d'autres classes de cartes bicolorées, en particulier reliées au modèle d'Ising et aux surfaces de translation.