Erdős-Rényi poissonnisé¶
L'objectif du court article de N.Curien est d'introduire une variante poissonnisée du graphe d'Erdős-Rényi. Un processus d'exploration très naturel est introduit, et il est simple à analyser. Ceci fournit des preuves très courtes de résultats classiques, ici on se concentre sur l'analyse de la transition de phase dite de la "composante géante", i.e. la transition en $p_n=c/n$.
On fixe $p,\alpha\in (0,1)$, et on définit le graphe aléatoire $G=G_{\mathrm{Poi}}(\alpha,p)$ de la façon suivante :
- On tire $N\sim \mathrm{Poi}(\alpha)$.
- L'ensemble des sommets de $G$ est $\{w_1,\dots,w_N\}\cup \{v_0,v_1,\dots \}$.
- Les sommets $\{w_1,\dots,w_N\}$ sont reliés entre eux par un Erdős-Rényi de paramètre $p$. Le sous-graphe résultant est appelé le core (traduction = noyau? coeur?)
- Les sommets $\{v_0,v_1,\dots \}$ constituent la pile. Chaque sommet de la pile est relié à chaque sommet du core avec probabilité $p$.
Tout ce qui est au-dessus (les arêtes du core, les arêtes core $\leftrightarrow $ pile) est indépendant de tout (conditionnellement à $N$).
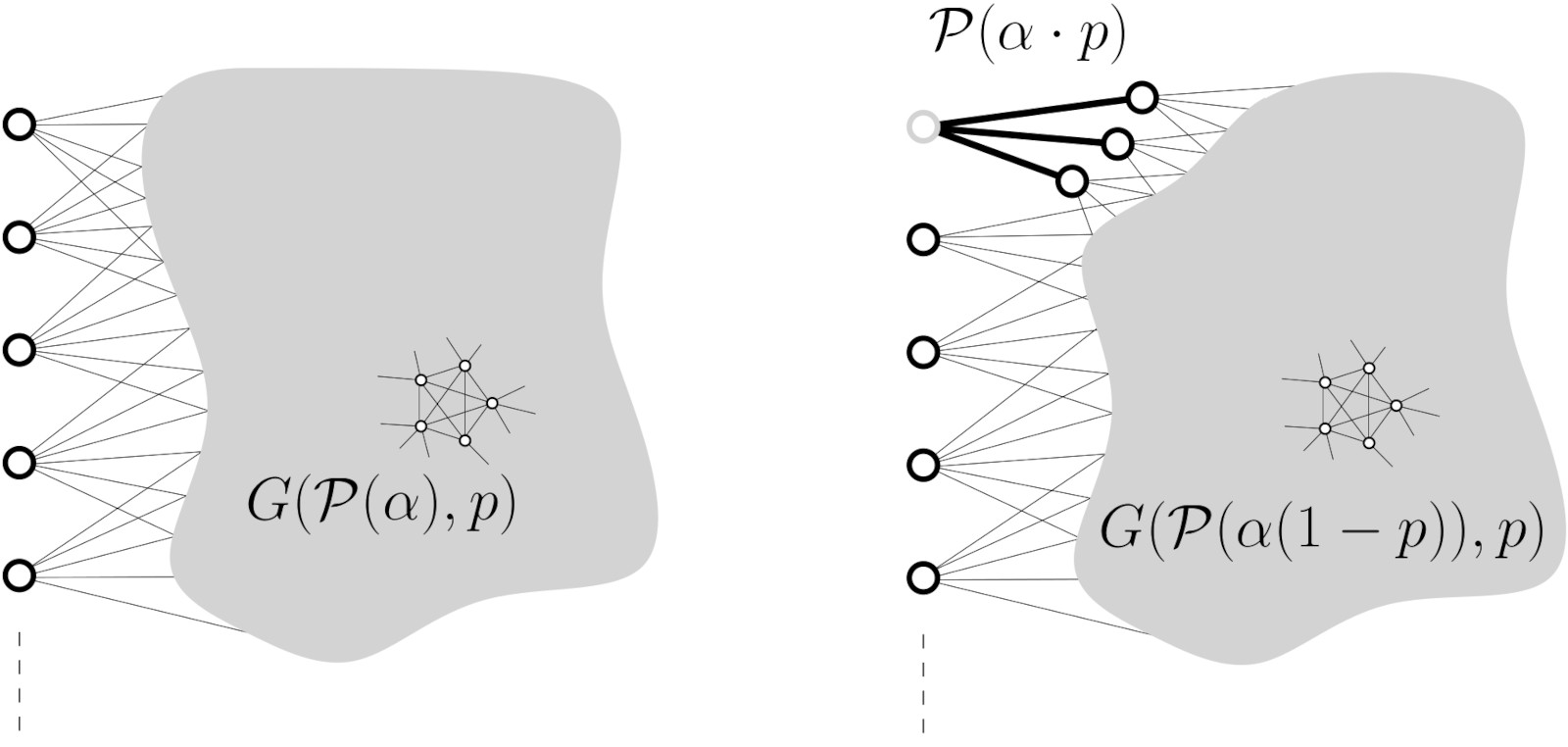
On introduit alors un processus (récursif) d'exploration sur $G_{\mathrm{Poi}}(\alpha,p)$:
- On retire $v_0$ de la pile.
- On ajoute dans la pile tous les voisins $y_1,\dots ,y_K$ de $v_0$. (Au passage, conditionnellement à $N$ on a $K\sim \mathrm{Binom}(N,p)$ et donc $K\sim \mathrm{Poisson}(\alpha p) $.)
- On retire $y_1,\dots y_K$ du core (ainsi que toutes les arêtes entre ces sommets).